Fork me on GitHub

Graph Theory

Posted on

Introduce some basic concepts and algorithms about graph theory.

Basic Concept

A Graph is, in its simplest form, a collection of points joined together in pairs by lines. In the jargon of the field the points are referred to as vertices or nodes and the lines are referred to as edges.
Terms:
1) Vertex = Node = Point = Actor
2) Edge = Line

Representation

1. Adjacency Matrix

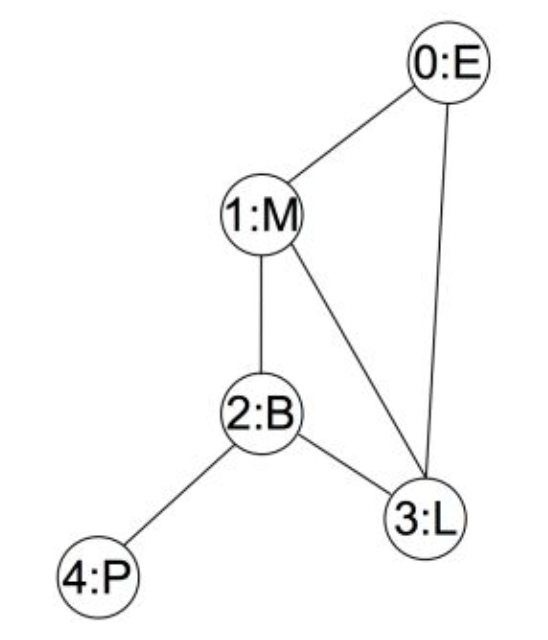
2. Adjacency List

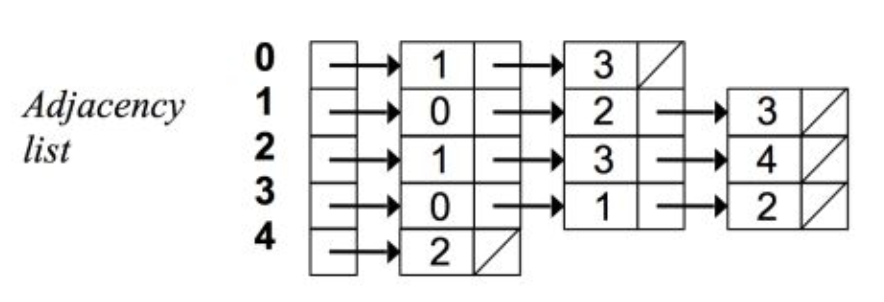
3. Comparison

The adjacency matrix saves search time and the adjacency list saves space.

1] Visit vertex v.
2] Choose an adjacency vertex to DFS.
3] Repeart step #1,2 until all vectices are visited.

1
2
3
4
5
def DFS(v):
  visit[v] = 1
  for w in range(n):
    if graph[v][w] == 1 and not visit[w]:
      DFS(w)

1] Visit vertex v.
2] Visit all adjacency vertices of v, and put them in the queue Q.
3] Visit v_news in V_new.
4] For v_new in Q, repeat step #2,3 until queue is null.

1
2
3
4
5
6
7
8
9
10
def BFS(v):
  visit[v] = 1
  queue = Queue.Queue()
  queue.put(v)
  while not queue.empty():
    queue.get()
    for w in range(n):
      if graph[w][v] == 1 and not visit[w]:
        visit[w] = 1
        queue.put(w)

Algorithm

1. Shortest Path Algorithm

1) Floyd
Floyd algorithm is used to calculate the shortest distance between two auxiliary vertices. The step is:
1] Initialize adjacency matrix and distances.
2] For vertex i, check whether exists vertex k to set up Dis(i,k) + Dis(k,j) < Dis(i,j). If so, update Dis(i,j) = Dis(i,k) + Dis(k,j).
3] Repeat 2] until all vertices have been went through.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <stdio.h>
int main() {
    int e[10][10]; // Adjacency Matrix.
    int k, i, j, n, m, t1, t2, t3;
    int inf = 99999999; // Infinity.
    // Input n, m, represnt number of vertices and number of edges respectively.
    scanf("%d %d", &n, &m);

    // Initialization.
    for (i = 1; i <= n; i++)
        for (j = 1; j <= n; j++)
            if (i == j) e[i][j] = 0;
              else e[i][j] = inf;
    
    // Input weight of edges.
    for (i = 1; i <= m; i++) {
        scanf("%d %d %d", &t1, &t2, &t3);
        e[t1][t2] = t3;
    }

    // Floyd.
    for (k = 1; k <= n; k++)
        for (i = 1; i <= n; i++)
            for (j = 1; j <= n; j++)
                if (e[i][j] > e[i][k] + e[k][j])
                    e[i][j] = e[i][k] + e[k][j];

    // Output results.
    for (i = 1; i <= n; i++) {
     	for (j = 1; j <= n; j++) {
            printf("%10d", e[i][j]);
        }
        printf("\n");
    }
    return 0;
}

2) Dijkstra
Dijkstra algorithm is used to calculate the shortest single source path.
The step is:
1] Initialize adjacency matrix and shortest distance array(between first vertex and others).
2] Initialize two sets U and V, represent shortest path vertex collection/remain vertex. First, add the first vertex to U. Others have been put to V.
3] Compare the distance between the first vertex and vertices belong to set V to find the shortest one. Then add corresponding vertex to U.
4] If dis[v] > dis[u] + e[u][v], update dis[v] = dis[u] + e[u][v].
5] Repeat 3] 4] until all vertices are added to U namely none nodes in V.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <stdio.h>
int main() {
    int e[10][10], dis[10], book[10] // Adjacency matrix，shortest distance, mark array.
    int i, j, n, m, t1, t2, t3, u, v, min;
    int inf = 99999999999; // Infinity.
    // Input n and m as number of vertices and edges respectively.
    scanf("%d %d", &n, &m);

    // Initialize adjacency matrix.
    for (i = 1; i <= n; i++)
        for (j = 1; j <= n; j++)
            if (i == j) e[i][j] = 0;
              else e[i][j] = inf;

    // Input weights of edges.
    for (i = 1; i <= m; i++) {
        scanf("%d %d %d", &t1, &t2, &t3);
        e[t1][t2] = t3;
    }

    // Initialize shortest distance array(between the first one and others).
    for (i = 1; i <= n; i++)
        dis[i] = e[1][i];

    // Initialize mark array.(be able to replace book[i] with dis[i]=0)
    for (i = 1 ; i <= n; i++)
        book[i] = 0;
    book[1] = 1;

    // Dijkstra.
    for (i = 1; i <= n-1; i++) {
        min = inf;
        // Find the distances between the first vertex and others.
        for (j = 1; j <= n; j++) {
            if (book[j] == 0 && dis[j] < min) {
                min = dis[j];
                u = j;
            }
        }
        book[u] = 1;
        // Update distances.
        for (v = 1; v <= n; v++) {
            if (e[u][v] < inf) {
                if (dis[v] > dis[u] + e[u][v])
                    dis[v] = dis[u] + e[u][v];
            }
        }
    }
    // Output results.
    for (i = 1; i <= n; i++)
        printf("%d ", dis[i]);
    return 0;
}

2. Minimum Spanning Trees

1) Prime
Prime solves the Minimum Spanning Tree problem of weight connected graph. The step is:
1] Initialize G = <V, E>, and set U contains vertices of MST. So (V-U) includes other vertices. And set T stores edges of MST. First add a random vertex u to U.
2] Choose a vertex u of U and sort the distances between u and other alters. Choose the shortest one (u, v). Add v to U and add (u, v) to T.
3] Repeat 2] until U = V.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <stdio.h>
int main() {
    int e[10][10]; // Adjacency Matrix.
    int prime[10], weights[10] // Prime result, weight of any other edges.
    int k, i, j, n, m, t1, t2, t3, min, index=0;
    int inf = 99999999; // Infinity.
    // Input n, m, represnt number of vertices and number of edges respectively.
    scanf("%d %d", &n, &m);

    // Initialization.
    for (i = 1; i <= n; i++)
        for (j = 1; j <= n; j++)
            if (i == j) e[i][j] = 0;
              else e[i][j] = inf;
    
    // Input weight of edges.
    for (i = 1; i <= m; i++) {
        scanf("%d %d %d", &t1, &t2, &t3);
        e[t1][t2] = t3;
    }
    
    // Weights between MST and other vertices.
    for (i = 1; i <= n; i++) {
        weights[i] = e[1][i];
    }

    // Prime.
    for (i = 1, i <= n; i++) {
        j = 1, k = 1;
        min = inf;
        while (j <= n) {
            if (weights[j] != 0 && weights[j] < min) {
                min = weights[j];
                k = j;
            }
            j++;
        }
        // Add kth vertex into MST set.
        prime[index++] = weights[k];
        weights[k] = 0;
        // Update weights.
        for (j = 1; j <= n; j++) {
            if (weights[j] != 0 && e[k][j] < weights[j])
                weights[j] = e[k][j];
        } 
    }

    // Output results.
    for (i = 0; i < n; i++) {
        totalWeight += primes[i];
    }
    printf("totalWeight = %d", totalWeight);
    return 0;
}

2) Kruskal
Do the same thing as Prime.
1] Sort all the edges in non-decreasing order of their weight.
2] Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it.
3] Repeat step#2 until there are (V-1) edges in the spanning tree.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <stdio.h>

// Adjacency matrix.
typedef struct _graph {
    char vexs[MAX];       // vertex
    int vexnum;           // number of vertices
    int edgnum;           // edges
    int matrix[MAX][MAX]; // adjacency matrix
}Graph, *PGraph;

// Edge struct.
typedef struct _EdgeData {
    char start; // start of edge
    char end;   // end of edge
    int weight; // weight of edge
}EData;

void kruskal(Graph G) {
    int i,m,n,p1,p2;
    int length;
    int index = 0;          // index of rets
    int vends[MAX]={0};     // stores the ends of each vertex of MST
    EData rets[MAX];        // result array, stores edges
    EData *edges;           // all edges

    // Get all the edges of graph.
    edges = get_edges(G);
    // Sort in descending order of weight.
    sorted_edges(edges, G.edgnum);

    for (i = 0; i < G.edgnum; i++) {
        p1 = get_position(G, edges[i].start);   // Get the number of start node of ith edge
        p2 = get_position(G, edges[i].end);     // Get the number of end node of ith edge
        m = get_end(vends, p1);                 // get end of p1
        n = get_end(vends, p2);                 // get end of p2
        // if m != n，means there is no cycle.
        if (m != n) {
            vends[m] = n;                       // set [end of m] = n
            rets[index++] = edges[i];           // store result
        }
    }
    free(edges);

    // Count and print.
    length = 0;
    for (i = 0; i < index; i++)
        length += rets[i].weight;
    printf("Kruskal=%d: ", length);
    for (i = 0; i < index; i++)
        printf("(%c, %c) ", rets[i].start, rets[i].end);
    printf("\n");
}

Reference