Network Generate Model and Algorithm

Introduce some network models and their generating algorithms.

ER Model

The Erdős–Rényi model is either of two closely related models for generating random graphs.

In the model of Erdős and Rényi, all graphs on a fixed vertex set with a fixed number of edges are equally likely; in the model introduced by Gilbert, each edge has a fixed probability of being present or absent, independently of the other edges.

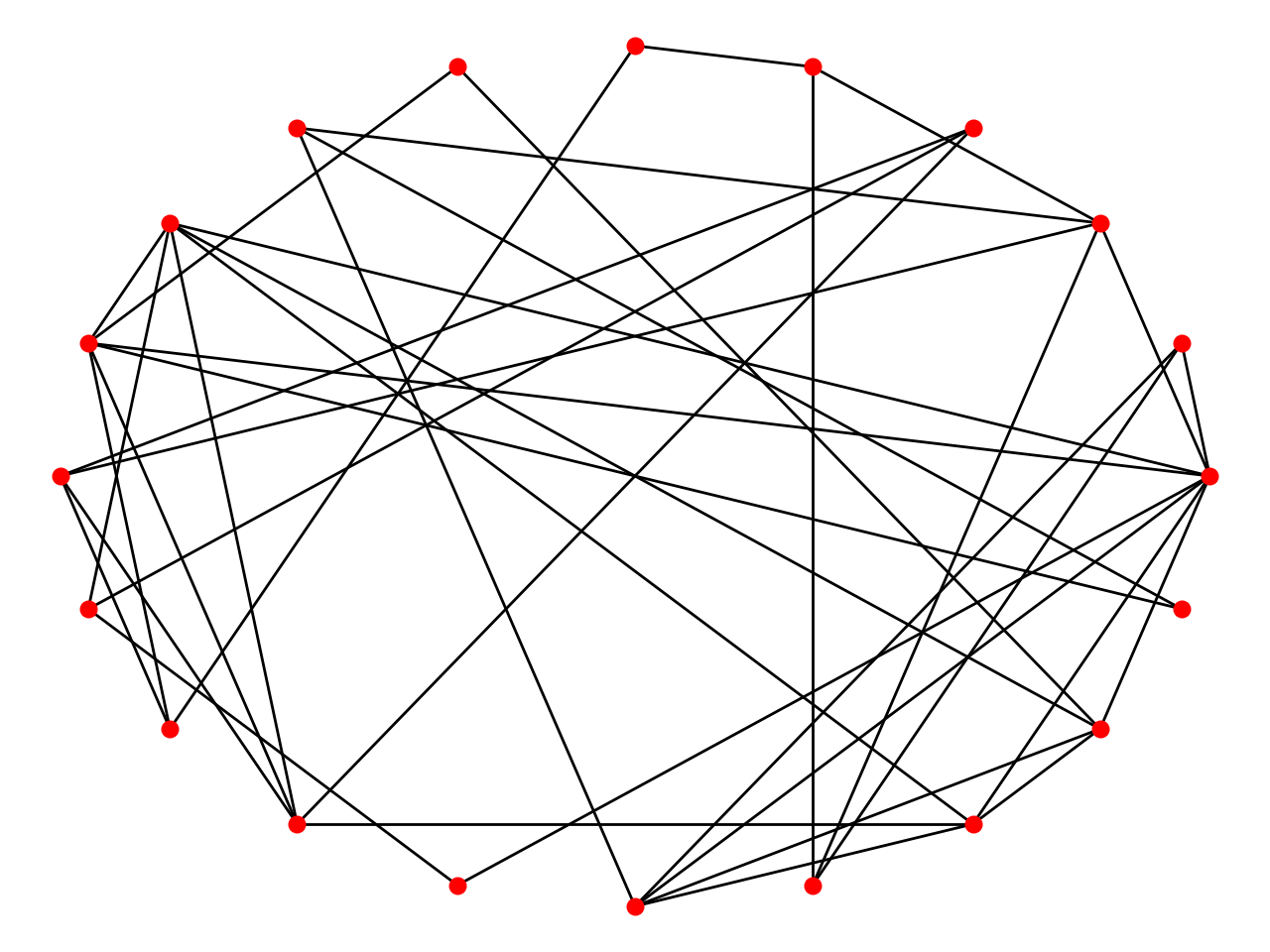
Algorithm

1. Initialize adjacency matrix and probabilty p of linking.
2. For all pairs of vertices, generating a random number~(0, 1). If this number is larger than p, add a edge between this pair of vertices.
3. Do # step 2 until all vertices are choosed.

An efficient way to implement:

def generateERGraph(graph_size, probability):
  """Generate a random Erdős-Rényi undirected graph.

  Args:
    graph_size: Number of nodes in the graph.

  Returns:
    graph: Adjacency matrix of the graph.
  """

  # Initialize graph(represented by adjacency matrix).
  n = graph_size
  graph = np.zeros([n, n])
  w = -1
  lp = math.log(1.0 - probability)

  # Nodes in graph are from 0, n-1 (start with v as the second node index).
  v = 1
  while v < n:
    lr = math.log(1.0 - random.random())
    w = w + 1 + int(lr / lp)
    while w >= v and v < n:
      w = w - v
      v = v + 1
    if v < n:
      graph[v, w] = graph[w, v] = 1
  return graph

WS Small World Model

The Watts–Strogatz model is a random graph generation model that produces graphs with small-world properties, including short average path lengths and high clustering.

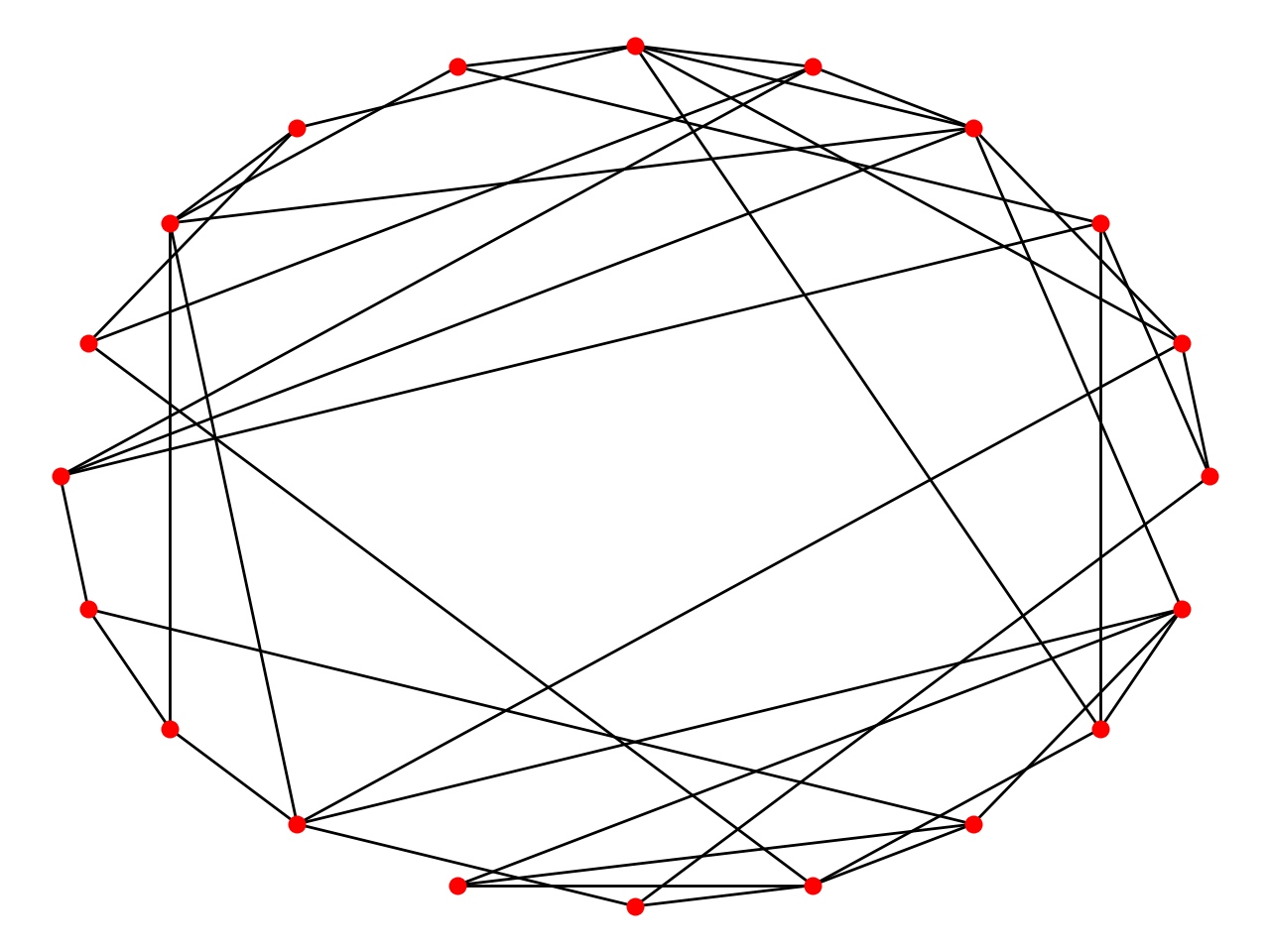
Algorithm

1. Initialize adjacency matrix, number of edges with neighbors and probabilty p of linking.
2. Connect each node to its right k/2 neighbors.
3. For each edge u-v in ring, with p, randomly selecting existing node w and add new edge u-w.

def generateSmallWorldGraph(graph_size, num_neighbors):
  """Generate a Watts–Strogatz small world graph.
	
  Args:
    graph_size: Number of nodes in the graph.
    num_neighbors: Number of edges with neighbors.
	
  Return:
    graph: Adjacency matrix of the graph.
  """
	
  # Initialize graph(represented by adjacency matrix).
  n = graph_size
  k = num_neighbors
  graph = np.zeros([n, n])
	
  nodes = range(n) # List of 0~n-1
  fromv = nodes
	
  # Connect each node to its right k/2 neighbors.
  for i in range(1, k//2+1):
    tov = fromv[i:] + fromv[:i]
    for j in range(n):
      graph[fromv[j], tov[j]] = graph[tov[j], fromv[j]] = 1
	
  # For each edge u-v in ring, with PROBABILITY, randomly selecting
  # existing node w and add new edge u-w.
  for u in range(n):
    degree_u = calculateDegree(graph, u)
    for v in range(n):
      if graph[u][v] > 0 and PROBABILITY > np.random.rand():
        w = np.random.randint(n)
        while u == w or graph[u][w] > 0:
          w = np.random.randint(n)
          if degree_u >= n-1:
            break
        else:
          graph[u][w] = graph[w][u] = 1
	
  return graph
  
def calculateDegree(graph, vertex):
  """Calculate degree of the node in the graph.
	
  Args:
    graph: Adjacency matrix.
    vertex: Node ID.
	
  Returns:
    degree: Degree of the node.
  """
  n = len(graph)
  degree = 0
  for j in range(n):
    if graph[vertex][j] > 0:
      degree += 1
  return degree

BA Model

The Barabási–Albert (BA) model is an algorithm for generating random scale-free networks using a preferential attachment mechanism.

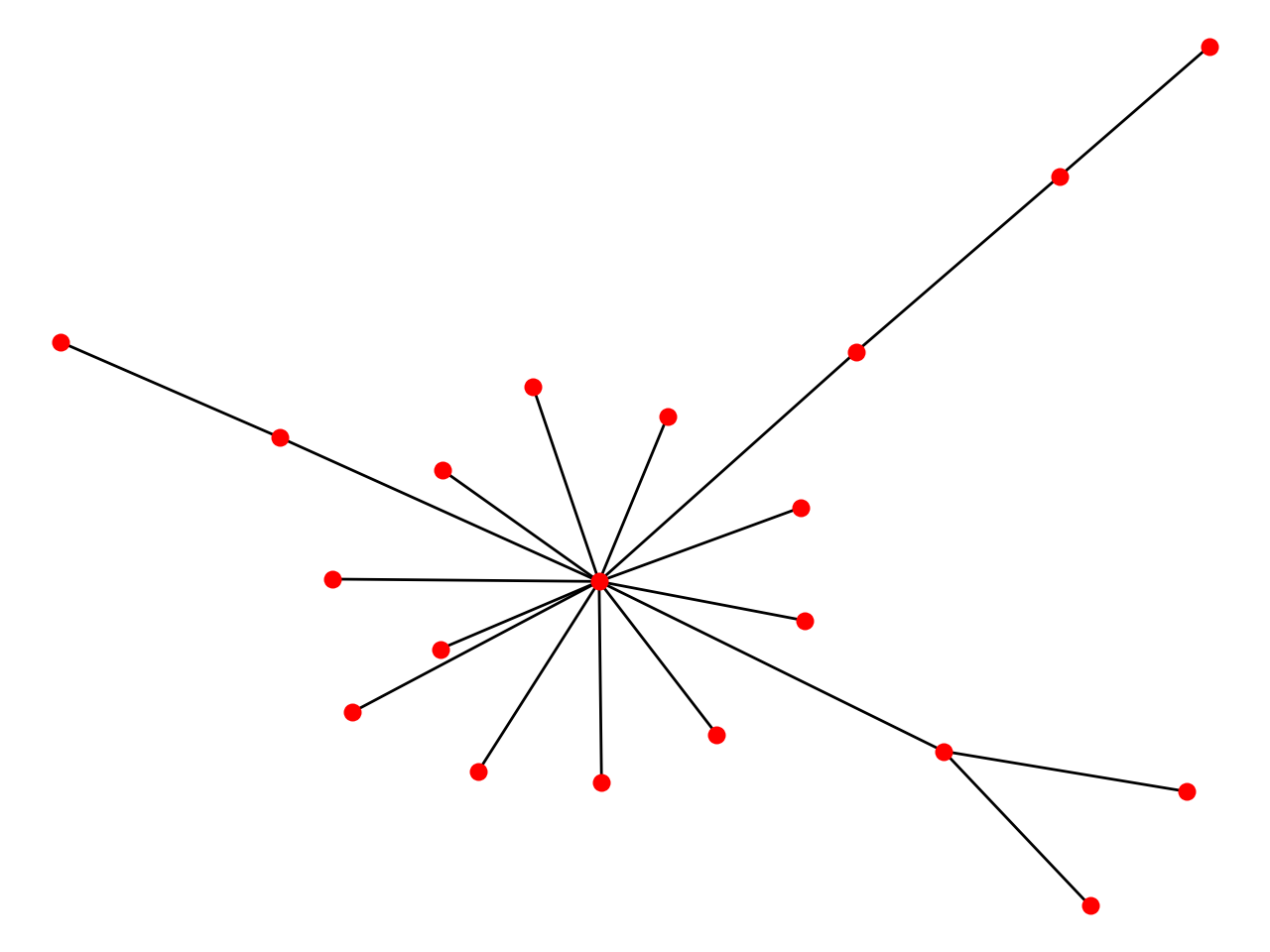
Algorithm

1. Initialize adjacency matrix and number of edges to attach from a new node to existing nodes. Choose a initial vertex v, a target list and a repeated list both with size m.
2. Link v and vertices from target.
3. Add [v]*m and all vertices from target to repeated list.
4. Update target list by randomly choosing m vertices from repeated list and then choose a new vertex v to go # step 2.

def generateBAGraph(graph_size, num_new_edges):
  """Generate a Barabási–Albert preferential attachment model graph.
	
  Args:
    graph_size: Number of nodes in the graph.
    num_new_edges:  Number of edges to attach from a new node to existing nodes.
	
  Returns:
    graph: Adjacency matrix of the graph.
  """
	
  # Initialize graph(represented by adjacency matrix).
  n = graph_size
  m = num_new_edges
  graph = np.zeros([n, n])
	
  targets = range(m) # Target nodes for new edges
  repeated_nodes = [] # List of existing nodes
	
  # Start adding edge from m.
  source = m
  while source < n:
    # Link target nodes and source.
    for i in range(m):
      graph[source, targets[i]] = graph[targets[i], source] = 1
	
    # Add target to repeated list(each node has been linked once).
    repeated_nodes.extend(targets)
	
    # Add source to repeated list(each node has been linked once).
    repeated_nodes.extend([source] * m)
	
    # Randomly get m nodes from repeated list to form new target.
    targets = random.sample(repeated_nodes, m)
    source += 1
	
  return graph